Epsilon Delta Definition of Continuity Explained

Alternative definition of continuity

There are two basic ways to approach continuity. One is the approach we adopted here in Math Tutor, continuity is defined using the notion of limit. However, it is also possible to define continuity without the use of limit, which is "cleaner" from theoretical point of view. Therefore some more theoretically inclined mathematicians prefer this alternative approach and we will show it here, since there is a chance that some students will encounter it.

The definition goes as follows.

Definition.
Let f be a function defined on some neighborhood of a point a. We say that the function f is continuous at a if for every ε > 0 there exists δ > 0 such that for all x from D(f ) satisfying |x −a| < δ we have |f (x) −f (a)| <ε.

Let's try to translate this into "normal language". This definition is essentially a game (the popular "epsilon-delta" game), similar to the one we considered when trying to understand the concept of a limit. We are the ones trying to show that the given function is continuous at a given point. Our opponent is trying to spoil it for us. He gives us a tolerance ε. Our task is to make sure that the function does not move away from the value f (a) by more than the given ε, and the tool we use for it is to restrict the graph of f to some piece around this given point. Technically we do it by specifying by how much one can move left or right from a without the graph getting out of the tolerance; this it the δ. In other words, we have to specify a certain neighborhood of a on which the function is within the given tolerance.

Mathematically, somebody gives us the tolerance ε. We have to find a δ so that if we take any x from the domain D(f ) which satisfies |x −a| < δ, then the function value at x stays within the given tolerance from f (a) - mathematically, |f (x) −f (a)| <ε. If we can do it, we win the game; for continuity to be true we have to be able to win all possible games, for any possible value of epsilon that somebody gives us.

Now recall two examples from the section on continuity.

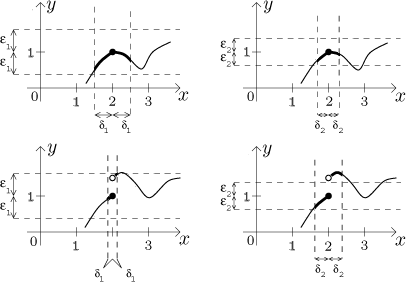
How does the definition with with them? In the following picture we tried to show two such games for each function. For two different epsilons we tried to find the corresponding deltas, we always made the parts of the graph that correspond to the choice of delta thicker. In the first example (the first row of pictures) it seems that no matter what epsilon we are given, even if it were incredibly small, we can still find a suitable delta so that the corresponding part of the graph lies in the strip given by the tolerance epsilon around the level 1 =f (2), and so win the game; this suggests that the left function is continuous at a = 2 by the defintion. On the other hand, in the second row we looked at the function that was on the right and we see that although we were able to win some games, we lost when epsilon got too small. No matter how small a neighborhood around a we choose, there will always be points in this neighborhood which, when substituted into f, will cause f to jump out of the given tolerance. Thus this second function is not continuous at a = 2 by the definition.

Note that both inequalities in the definition can be nicely written using neighborhoods. The continuity condition then looks much neater, it goes like this: For every ε > 0 there exist δ > 0 such that for all x∈U _δ(a) ∩D(f ) we have f (x)∈U _ε (f (a)). As you can imagine, mathematicians, familiar with this notation, definitely prefer this shorter way. In fact, they would go even further. Here is the most general definition of continuity at point a which works for all functions, not just the real ones: For every neighborhood V of f (a) there must exist a neighborhood U of a such that f (U ∩D(f ))⊆V.

Similarly we define one-sided continuity, we just have to restrict those x to an appropriate side of a.

Definition.
Let f be a function defined on some left neighborhood of a point a. We say that the function f is continuous from the left at a if for every ε > 0 there exists δ > 0 such that for all x from D(f ) satisfying a − δ <x ≤a we have |f (x) −f (a)| <ε.
Let f be a function defined on some right neighborhood of a point a. We say that the function f is continuous from the right at a if for every ε > 0 there exists δ > 0 such that for all x from D(f ) satisfying a ≤x <a + δ we have |f (x) −f (a)| <ε.

The definition of continuity, especially its game nature, should have reminded you of the definition of a limit. In fact, it is almost exactly the same. The only difference in the mantra "for every... there is..." is that in the definition of the limit we did not allow x to be a, whereas here in the continuity case also the a is included in the game. From this one can deduce the following fact:

Theorem.
Consider a function f. This function is continuous at a from the left if and only if it has a limit at a from the left and this limit is equal to f (a).
Consider a function f. This function is continuous at a from the right if and only if it has a limit at a from the right and this limit is equal to f (a).
Consider a function f. This function is continuous at a if and only if it has a limit at a and this limit is equal to f (a).

This shows that the alternative definition of continuity defines the same notion as the definition from our section on continuity.

This theorem should seem quite natural. When we introduced continuity a while back, we said that it is really a question whether the graph of f goes to some specific point as x approaches a, and this formulation should have already rang some bells. If you now recall the meaning of limit and read again the introduction above, it should all seem perfectly clear.

perezwimenceph.blogspot.com

Source: https://math.fel.cvut.cz/en/mt/txtb/3/txe4ba3d.htm

Share this post